How To Generate Random Numbers In SQL Server?

In SQL Server there is a built-in function RAND() to generate random number. RAND() will return a random float value between 0 to 1.

Usage RAND() As It Is

If you use RAND() as it is or by seeding it, you will get random numbers in decimals ranging between 0 and 1.

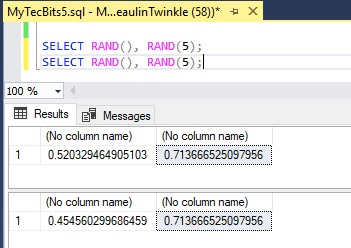
SELECT RAND(), RAND(5);
SELECT RAND(), RAND(5);

/* Result */
0.5651861527384644            0.713666525097956
0.454560299686459             0.713666525097956

Generate Integer Random Number Between Two numbers

In case if you want random numbers generated between two integers then use this syntax:

Syntax

A + FLOOR(RAND() * (B + 1 - A));
Where:
A = The smallest number of the range.
B = The largest number of the range.

Example

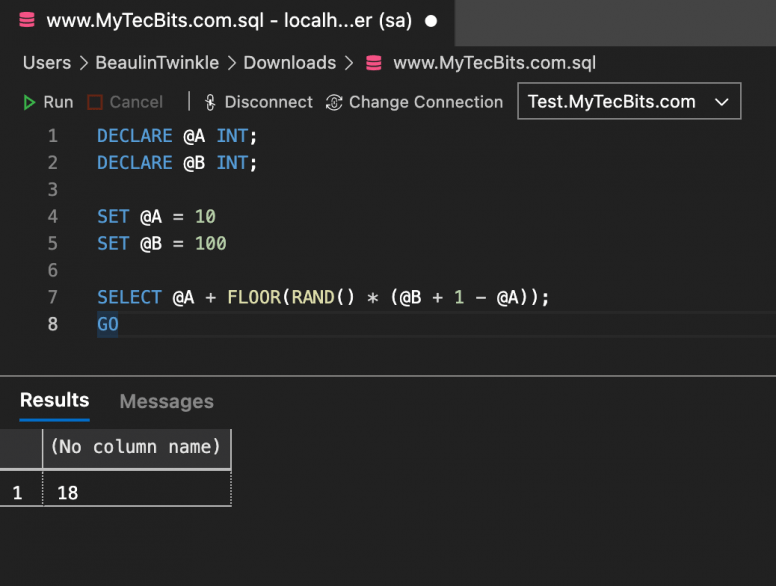
DECLARE @A INT;
DECLARE @B INT;
 
SET @A = 10
SET @B = 100
 
SELECT @A + FLOOR(RAND() * (@B + 1 - @A));
GO

/* Result */
73

Generate Random Integer Between 0 And Any Integer

For generating random integer between 0 to any number use this formula:

Syntax

ROUND(RAND() * A, 0);
Where:
A = The largest number of the range.

Example

This script will generate random integer between 0 to 100

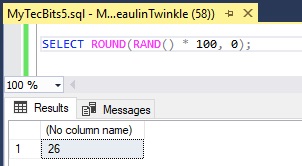
SELECT ROUND(RAND() * 100, 0);
GO

/* Result */
26

Generate Random Float Between 0 And Any Number

To generate random float number between 0 and any number use this formula:

Syntax

RAND() * A;
Where:
A = The largest number of the range.

Example

This script will generate random float number between 0 to 100

SELECT RAND() * 100;

/* Result */
27.787772112756

Reference

• About RAND() math function at Microsoft Docs.