Advanced Fibonacci Number Calculator

This advanced Fibonacci number calculator can accept arbitrary first and second term and provides you the Fibonacci number of the given n^th term. You can find Fibonacci number for up to its 10,000^th term. So, you do not need to do manual additions or other calculations to find the Fibonacci numbers up to F_10,000.

Using This Calculator

Follow these steps to generate a Fibonacci Number:

1. Enter the First Term (F₀) of the Fibonacci Sequence.
2. Enter the Second Term (F₁) of the Fibonacci Sequence.
3. Enter the n^th term index. This field accepts input up to 10,000.
4. Finally press the Find Fibonacci Number button.
5. The result will be displayed below the button.

Example

If you want to find the Fibonacci Number of 100^th term (F₁₀₀) with an arbitrary starter of F₀ = 10 and F₁ = 20, then enter 10 in the First Term (F₀) field, 10 in the Second Term (F₁) field and enter 100 in the n field. Finally press the Find Fibonacci Number button.

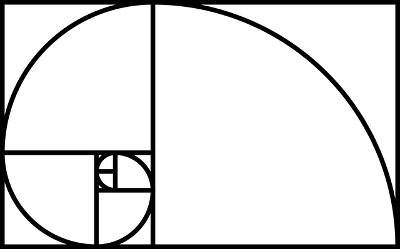
Fibonacci Numbers or Fibonacci Sequence

Fibonacci sequence is a series of numbers in mathematics which follows a specific pattern. Fibonacci numbers are denoted by the term F_n. Every number in the Fibonacci sequence is the sum of the two preceding Fibonacci numbers. Now, let us see the formula used to generate the Fibonacci Sequence.

Formula For Fibonacci Sequence With arbitrary Starters

The formula used to generate Fibonacci Series F_n is:

F_n = F_n-2 + F_n-1

where:

• F₀ = a
• F₁ = b
• a and b are the arbitrary starters.
• n > 1

Using the Formula

1. Let us consider the first term (F₀) in the Fibonacci sequence is 10.
2. The second term (F₁) in the Fibonacci sequence is 20.
3. To find the remaining terms, you have to apply the formula (F_n = F_n-2 + F_n-1).
4. So, F₂ = F₀ + F₁.
     i.e. F₂ = 10 + 20 = 30.
5. Likewise, F₃ = F₁ + F₂.
     i.e. F₃ = 20 + 30 = 50.
6. Thus, the first 10 terms of this Fibonacci series with arbitrary starters are 10, 20, 30, 50, 80, 130, 210, 340, 550, 890,... Use the above calculator to generate more Fibonacci numbers with arbitrary starters.

Formula For n^th Fibonacci Number

There is a simpler way to find the n^th term alone of the Fibonacci sequence using the golden ratio.

The formula used to find the n^th term F_n with arbitrary starters is:

F_n = xΦⁿ + yΨⁿ
x = (F₁ - F₀Ψ) ÷ √5
y = (ΦF₀ - F₁) ÷ √5

where:

• F₀ is the first arbitrary term.
• F₁ is the second arbitrary term.
• Φ is the golden ratio.
• Φ = (1 + √5) ÷ 2
• Ψ = 1 - Φ = (1 - √5) ÷ 2
• n > 1

• About Fibonacci series in wikipedia.org