Statistical Mean, Median and Mode Calculator
Online calculator to find the statistical mean, median and mode for the given set of data. This calculator also gives you the minimum, maximum, count and sum of the elements of the dataset.
Enter the numbers separated by commas and press the Calculate button to get the result.
About Statistical Mean, Median and Mode Calculator
This Statistical Mean, Median and Mode Calculator takes a dataset of comma separated numbers and calculates the statistical mean, median and mode of the data set. This calculator also calculates the minimum value, maximum value, count of elements in the dataset and the sum of the numbers in the set.
Using Statistical Mean, Median and Mode Calculator
- Enter the Data Set in comma separated format.
- Press the Calculate button to get the result.
Concepts & Formulas
Arithmetic Mean
Arithmetic mean is the average of the collection of numbers (dataset). It is calculated by adding all the numbers in the collection and divided by the count of numbers in the collection. i.e. mean is the average of numbers in the dataset.
Formula
Let's call the collection of numbers { x1, x2, ... , xn } as x. The arithmetic mean be x.
The formula to find arithmetic mean x is:
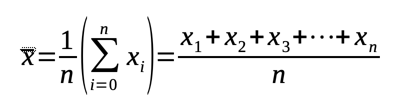
Example:
If x = { 1, 2, 3, 4, 5},
then n = 5.
So, mean x = ( x1 + x2 + ... + xn ) / n = (1 + 2 + 3 + 4 + 5) / 5 = 3
Median
Median is the middle value of the given dataset of numbers arranged in an order form lower to higher value.
Formula
Consider a data set x = { x1, x2, ... , xn }.
For odd number of elements:
If "n" is an odd number (i.e. the dataset has odd number of elements) then:
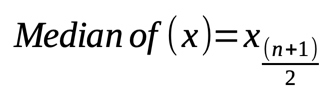
Example:
If x = { 1, 2, 3, 4, 5},
then n = 5.
So, Median of (x) = x(n + 1) / 2 = x(5 + 1) / 2 = x3 (i.e. 3rd element) = 3
For even number of elements:
If "n" is an even number (i.e. the dataset has even number of elements) then:
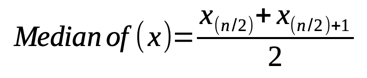
Example:
If x = { 1, 2, 3, 4, 5, 6},
then n = 6.
So, Median of (x) = [x(n / 2) + x(n / 2) + 1] / 2 = (x3 + x4) / 2 = (3 + 4) / 2 = 3.5
Mode
In mathematical statistics, the value which appears most often in the given collection of numbers is called a mode of the data set. Based upon the number of modes, a data set can have one mode (unimodal) or multiple modes (bimodal, trimodal or multimodal).
Unimodal dataset
In the dataset {1, 2, 3, 4, 5, 4, 2, 2}, you can see that element 2 is repeated the most number of times. So the mode of this dataset is 2.
Bimodal dataset
In the dataset {1, 2, 3, 4, 5, 4, 2, 2, 4}, you can see the elements 2 and 4 are repeated the most number of times, three times each. So the modes of this dataset are 2, 4.
Multimodal dataset
In the dataset {1, 2, 3, 4, 5, 4, 2, 2, 4, 1, 1}, you can see the elements 1, 2 and 4 are repeated the most number of times, three times each. So the modes of this dataset are 1, 2, 4.
No mode dataset
In the dataset {1, 2, 3, 4, 5}, all the elements are equally spread. So, there is no mode in this dataset.
Minimum
The smallest value in the dataset is the minimum of the dataset.
Maximum
The largest value in the dataset is the maximum of the dataset.
Count
Count is the number of elements in the dataset.
Sum
The sum of the dataset is the total of all the elements in the dataset.
Formula
If the dataset is represented as { a1, a2, ... , an }, then, sum = a1 + a2 + ... + an.
| Sum = | 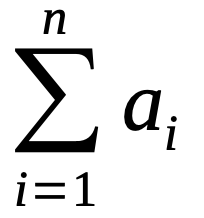 |
Reference
- C# program to calculate mean.
- C# program to calculate mean.
- C# program to calculate mode.
- More about arithmetic mean at wikipedia.
Page Last Modified On: Oct 14, 2022
Disclaimer: We took every effort to provide higher level of accuracy in the calculators, converters and tools we have added to www.MyTecBits.com Tools section. But, we cannot give any guarantee or can be held responsible for any errors, defects, faults or mistakes in any of the calculators, converters or tools. Please see detailed terms of use and liability disclaimer in Terms of Use Page.